Pembuktian Rumus Luas Persegi Panjang

Posted by Fandi on Thursday, December 19, 2013 in sains

Assalamu Alaikum,,

     Untuk membuktikan rumus luas persegi panjang, tidak jauh beda dengan cara membuktikan rumus luas persegi . Rumus luas persegi panjang ini pada dasarnya yaitu dari rumus Luas Persegi. Oleh karena itu, sebelumnya saya akan memberikan sebuah postulat, yaitu :
Postulat
     Daerah yang dilengkapi oleh persegi, dimana setiap sisinya memiliki panjang a, maka persegi ini memiliki luasan yang sama dengan a pangkat 2.

Kemudian dari postulat diatas menghasilkan sebuah teorema untuk Luas Persegi Panjang, yaitu :

Teorema

Luas suatu persegi panjang yang panjang sisinya a dan b adalah a.b

Bukti :
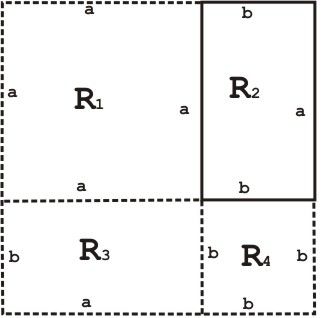
Misal kita konstruksikan Persegi Panjang dari suatu persegi seperti pada gambar dibawah ini.

dari gambar diatas dan menurut Postulat, maka :

(a + b)^2 = Luas R1 + Luas R2 + Luas R3 + Luas R4

a^2 + 2ab + b^2 = a^2 + Luas R2 + Luas R3 + b^2

karena Luas R2 = Luas R3, berakibat :
a^2 + 2ab + b^2 = a^2 + 2 Luas R2 + b^2
2a.b = 2 Luas R2
a.b = Luas R2 = Luas Persegi Panjang (TERBUKTI)

keterangan :  a^2 = a pangkat 2

Bagi yang ingin mendownload artikel di atas, silahkan klik DISINI