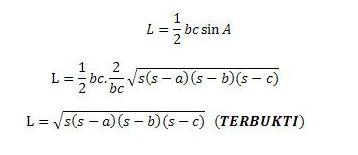Pembuktian Berbagai Rumus Luas Berbagai Segitiga

Posted by Fandi on Friday, December 20, 2013 in sains

Assalamu Alaikum,,

     Segitiga memiliki banyak rumus untuk mencari luasnya. Setiap rumus memiliki waktu tersendiri untuk menggunakannya, tergantung dari soal yang diberikan.

      Berikut  beberapa pembuktian rumus luas segitiga

1. pembuktian rumus L = 1/2 (alas x tinggi)

    terdiri dari beberapa kasus, yaitu :

Kasus 1 Untuk Segitiga Siku-Siku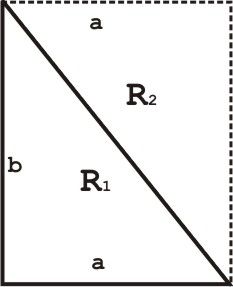



Luas Persegi Panjang = Luas R1 + Luas R2
a.b = 2 Luas R1 (karena Luas R1 = Luas R2)
1/2 (a.b ) = Luas R1
dengan a = alas dan b = tinggi
sehingga
L = (1/2) x alas x tinggi

Kasus 2 Untuk Segitiga Sama Kaki



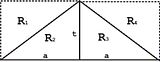
Luas Persegi Panjang = Luas R1 + Luas R2 + Luas R3 + Luas R4
2.a.t = 4 Luas R2 (karena Luas R1 = Luas R2 = Luas R3 = Luas R4)
2/4 (a.t) = Luas R1 = L
1/2 (a.t) = Luas R1 = L
dengan a := alas dan t := tinggi
sehingga
L = 1/2 (alas x tinggi)

Kasus 3 Untuk Segitiga Sembarang



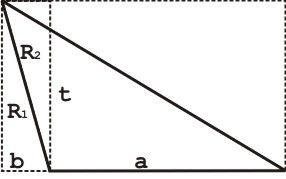
Luas Persegi Panjang = Luas R1 + Luas R2
Luas R1 + Luas R2 = b.t
karena Luas R1 = Luas R2, berakibat Luas R1 = 1/2(b.t)
1/2 ((a + b).t) = 1/2(b.t) + Luas
1/2(a.t) +1/2(b.t) –1/2(b.t) = Luas
1/2(a.t) = Luas
dengan a := alas dan t := tinggi
sehingga
L =1/2( alas x tinggi)

2. Pembuktian Rumus L = √(s (s-a )(s-b)(s-c))

PEMBUKTIAN
sin2 A + cos2 A = 1
sin2 A = 1 – cos2 A
sin2 A = (1 + cos A) (1 – cos A )
Ingat aturan cosinus:

Ingat bahwa s = ½ (a + b + c), maka
1. (a + b + c) = 2s
2. (b + c + a) = (a + b + c) – 2a = 2s – 2a = 2 (s – a )
3. (a + b – c) = (a + b + c) – 2c = 2s – 2c = 2 (s –c )
4. (a + c – b) = (a + c + b) – 2b = 2s – 2b = 2 (s –b )

Sehingga,

Ingat bahwa luas segitiga adalah:

3. Pembuktian Rumus L= ½ bc. sin A / ½ ac. sin B / ½ ab. sin C 

L = 1/2 (c.t)

karena t belum diketahui maka dapat dicari dengan

t/b = sin A

t = b sin A

sehingga L = 1/2 (c.t) = 1/2(c. b sin A) = 1/2 (bc sin A)

Begitupun untuk mencari rumus yang lain.

Bagi yang ingin mendownload, silahkan klik DISINI