Integral Tak Tentu :
Misalkan u = u(x) dan v = v(x), maka, rumus integral parsial untuk integral tak tentu adalah : Untuk mendapatkan rumus di atas kita mulai dengan mengingat kembali mengenai aturan turunan hasil kali dua fungsi, yaitu :
Misalkan u = u(x) dan v = v(x), maka, rumus integral parsial untuk integral tak tentu adalah : Untuk mendapatkan rumus di atas kita mulai dengan mengingat kembali mengenai aturan turunan hasil kali dua fungsi, yaitu :
dari persamaan diatas, kemudian kita
integralkan kedua ruas :
Pada
ruas kiri sangat mudah mengintegralkannya, karena (uv)’ merupakan turunan dari
uv, maka integral atau anti turunannya kembali akan menghasilkan uv. pada ruas
kanan, kita akan menggunakan salah satu sifat integral untuk dua fungsi yang
dijumlahkan, menghasilkan :
Kemudian,
kedua ruas di tambahkan
menghasilkan :
Kedua ruas di kalikan dengan (-1), menjadi
atau
Integral Tentu
:
Misalkan u = u(x) dan v = v(x),
maka, rumus integral parsial untuk integral tentu adalah :
Rumus ini bisa didapatkan dari aturan parsial pada
integral tak tentu. Telah diketahui bahwa rumus integrasi parsial pada integral
tak tentu adalah
Telah
diketahui juga bahwa uv didapatkan dari
jadi persamaan di atas dapat ditulis
kembali menjadi :
Setelah
itu, kita dapat memberikan batas – batas untuk setiap integral pada persamaan
diatas. Misalkan batasnya adalah dari a sampai
b.
Dengan
mengintegralkan
Persamaan di atas dapat diubah menjadi :
jika ingin mendownload "Penurunan Rumus Teknik Integral Secara Parsial " dalam PDF, silahkan klik link download di bawah :











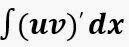









Tq ilmu yg bermanfaat
ReplyDelete