Posted by Fandi on Tuesday, December 10, 2013 in sains
Assalamu Alaikum,,

Sebagai mahasiswa matematika ataupun pelajar yang biasa mengikuti olimpiade matematika, tidak jarang kita akan bertemu soal-soal yang perlu di buktikan. Kebetulan saya selaku seorang mahasiswa matematika dari Universitas Sulawesi Barat sangat sering menemukan kasus seperti itu. Untuk itu, kali ini saya akan memberikan gambaran tentang 10 metode yang biasa di gunakan untuk membuktikan sebuah kasus / soal matematika.
Definisi memainkan peranan penting di dalam matematika. Topik-topik baru matematika selalu diawali dengan membuat definisi baru. Sebagai contoh, teori fungsi kompleks diawali dengan mendefinisikan bilangan imajiner i, yaitu i berpangkat 2 = -1. Berangkat dari definisi dihasilkan sejumlah teorema beserta akibat-akibatnya. Teorema-teorema inilah yang perlu dibuktikan. Pada kasus sederhana, kadangkala teorema pada suatu buku ditetapkan sebagai definisi pada buku yang lain, begitu juga sebaliknya. Selanjutnya, untuk memahami materi selanjutnya dibutuhkan prasyarat pengetahuan logika matematika. Ada beberapa metode dalam pembuktian matematika, diantaranya sebagai berikut :
1. Metode Pembuktian Langsung
Metode pembuktian langsung adalah suatu proses pembuktian pembuktian menggunakan alur maju, mulai dari hipotesis dengan menggunakan implikasi logic sampai pada pernyataan kesimpulan. Hukum-hukum dalam matematika pada umumnya berupa proposisi atau pernyataan berbentuk implikasi (p  q) atau biimplikasi (p
q) atau biimplikasi (p  q) atau pernyataan kuantifikasi yang dapat diubah bentuknya menjadi pernyataan implikasi. Misal kita punya teorema p
q) atau pernyataan kuantifikasi yang dapat diubah bentuknya menjadi pernyataan implikasi. Misal kita punya teorema p  q, dengan p disini sebagai hipotesis yang digunakan sebagai fakta yang diketahui atau sebagai asumsi. Selanjutnya, dengan menggunakan p kita harus menunjukkan bahwa berlaku q.
q, dengan p disini sebagai hipotesis yang digunakan sebagai fakta yang diketahui atau sebagai asumsi. Selanjutnya, dengan menggunakan p kita harus menunjukkan bahwa berlaku q.
contoh :
Buktikan, jika x bilangan ganjil maka x pangkat 2 bilangan ganjil.
Bukti :
Diketahui x ganjil, jadi dapat didefinisikan sebagai x := 2n + 1 untuk suatu n 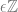 . Selanjutnya, x2 = (2n + 1)2 = 4n2 + 4n + 1 = 2 (2n2 + 2) + 1, dengan mengambil m := 2n2 + 2, m
. Selanjutnya, x2 = (2n + 1)2 = 4n2 + 4n + 1 = 2 (2n2 + 2) + 1, dengan mengambil m := 2n2 + 2, m 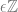 maka x2 = 2m + 1. Karena m merupakan bilangan bulat maka disimpulkan x2 ganjil.
maka x2 = 2m + 1. Karena m merupakan bilangan bulat maka disimpulkan x2 ganjil.
2. Metode Pembuktian Tak Langsung
Kita tahu bahwa nilai kebenaran suatu implikasi p  q ekuivalen dengan nilai kebenaran kontraposisinya ~q
q ekuivalen dengan nilai kebenaran kontraposisinya ~q  ~p. Jadi pekerjaan membuktikan kebenaran pernyataan implikasi dibuktikan lewat kontraposisinya.
~p. Jadi pekerjaan membuktikan kebenaran pernyataan implikasi dibuktikan lewat kontraposisinya.
contoh:
Buktikan, jika x2 (x pangkat 2) bilangan ganjil maka x bilangan ganjil.
Bukti. Pernyataan ini sangat sulit dibuktikan secara langsung. Mari kita coba saja. Karena x2 ganjil maka dapat ditulis x2 = 2m + 1 untuk suatu bilangan asli m. Selanjutnya x = tidak dapat disimpulkan apakah ia ganjil atau tidak. Sehingga bukti langsung tidak dapat digunakan. Kontraposisi dari pernyataan ini adalah ”Jika x genap maka x2 genap”. Selanjutnya diterapkan bukti langsung pada kontraposisinya. Diketahui x genap, jadi dapat ditulis x = 2n untuk suatu bilangan bulat n. Selanjutnya, x2 = (2n)2 = 2 (2n2) = 2m yang merupakan bilangan genap.
3. Metode Kontradiksi (Metode favorit saya, hehehehe,,)
Pembuktian melalui kontradiksi (bahasa Latin: reductio ad absurdum, 'reduksi ke yang absurd', bahasa Inggris: proof by contradiction, 'bukti oleh kontradiksi'), adalah argumen logika yang dimulai dengan suatu asumsi, lalu dari asumsi tersebut diturunkan suatu hasil yang absurd, tidak masuk akal, atau kontradiktif, sehingga dapat diambil kesimpulan bahwa asumsi tadi adalah salah (dan ingkarannya benar). Dalam disiplin matematika dan logika, pembuktian melalui kontradiksi merujuk secara khusus kepada argumen dimana sebuah kontradiksi dihasilkan dari suatu asumsi (sehingga membuktikan asumsi tadi salah) Argumen ini menggunakan hukum non-kontradiksi - yaitu suatu pernyataan tidak mungkin benar dan salah sekaligus.
contoh:
Contoh klasik pembuktian melalui kontradiksi pada zaman Yunani Kuno adalah pembuktian bahwa akar kuadrat dari duamerupakan bilangan irasional (tidak bisa dinyatakan sebagai perbandingan bilangan bulat). Pernyataan ini dapat dibuktikan dengan cara mengasumsikan sebaliknya bahwa √2 adalah bilangan rasional, sehingga bisa dinyatakan sebagai perbandingan bilangan bulat a/b dalam pecahan yang paling sederhana. Tapi jika a/b = √2, maka a2 = 2b2. Ini berarti a2 adalah bilangan genap. Karenakuadrat dari bilangan ganjil tidak mungkin genap, maka a adalah bilangan genap. Karena a/b adalah pecahan paling sederhana bpastilah ganjil (sebab pecahan genap/genap masih bisa disederhanakan). Namun karena a adalah bilangan genap (anggap 2r artinya a2 (4r2) adalah bilangan kelipatan 4, dan b2 adalah bilangan kelipatan 2 (genap). Hal ini berarti b juga merupakan bilangan genap, dan ini merupakan kontradiksi terhadap kesimpulan sebelumnya bahwa b pastilah ganjil. Karena asumsi awal bahwa √2 adalah rasional mengakibatkan terjadinya kontradiksi, asumsi tersebut pastilah salah, dan ingkarannya (bahwa √2 adalah irasional) merupakan pernyataan yang benar.
4. Metode "Bukti Kosong"
Bila hipotesis p pada implikasi p  q sudah bernilai salah maka implikasi p
q sudah bernilai salah maka implikasi p  q selalu benar apapun nilai kebenaran dari q. Jadi jika kita dapat menunjukkan bahwa p salah maka kita telah berhasil membuktikan kebenaran p
q selalu benar apapun nilai kebenaran dari q. Jadi jika kita dapat menunjukkan bahwa p salah maka kita telah berhasil membuktikan kebenaran p  q.
q.
contoh :
Didalam teori himpunan kita mengenal definisi berikut :“Diberikan dua himpunan A dan B. Himpunan A dikatakan himpunan bagian dari B, ditulis A ∈ B jika pernyataan berikut dipenuhi : ”jika x ∈ A maka x ∈ B”. Suatu himpunan dikatakan himpunan kosong jika ia tidak mempunyai anggota. Buktikan, himpunan kosong merupakan himpunan bagian dari himpunan apapun.”
Bukti. Misalkan A = ∅ suatu himpunan kosong dan B himpunan sebarang. Kita akan tunjukkan bahwa pernyataan ”jika x ∈ A maka x ∈ B” bernilai benar. Karena A himpunan kosong maka pernyataan p yaitu x ∈ A selalu bernilai salah karena tidak mungkin ada x yang menjadi anggota himpunan kosong. Karena p salah maka terbuktilah kebenaran pernyataan ”jika x ∈ A maka x ∈ B”, yaitu A ∈ B. Karena B himpunan sebarang maka bukti selesai.
5. Metode Pembuktian Trivial
Bila pada implikasi p  q, dapat ditunjukkan bahwa q benar maka implikasi ini selalu bernilai benar apapun nilai kebenaran dari p. Jadi jika kita dapat menunjukkan bahwa q benar maka kita telah berhasil membuktikan kebenaran p
q, dapat ditunjukkan bahwa q benar maka implikasi ini selalu bernilai benar apapun nilai kebenaran dari p. Jadi jika kita dapat menunjukkan bahwa q benar maka kita telah berhasil membuktikan kebenaran p  q.
q.
contoh :
Buktikan, jika 0 < x < 1 maka 0 < (1-x) . Bukti. Karena pernyataan q, yaitu 0 < (1-x) . selalu benar untuk setiap x bilangan real termasuk x di dalam interval (0, 1) maka secara otomatis kebenaran pernyataan ini terbukti.
6. Metode Pembuktian Ketunggalan
Pembuktian ini membutuhkan bukti eksistensial misal x, kemudian ambil sembarang objek misalnya y lalu tunjukkan bahwa y=x. Cara lain adalah dengan mengambil y yang tidak sama dengan y lalu tunjukkan kontradiksi
”Untuk setiap n bilangan asli maka merupakan bilangan prima”
Bukti. Pernyataan ini berlaku untuk setiap bilangan asli n. Tapi bila bila ditemukan satu bilangan asli, katakan n0 dan tidak prima (komposit) maka konjektur ini tidak benar. Diperhatikan beberapa kasus berikut, untuk n = 1 diperoleh bilangan 5, n = 2 menghasilkan 17, n = 3 mengahasilkan 257 dan n = 4 menghasilkan 65537. Keempat bilangan ini prima. Coba perhatikan untuk n = 5, diperoleh = 4294967297 = (641)(6700417). Ternyata bukan prima. n = 5 merupakan contoh penyangkalan (counter example). Akhirnya disimpulkan bahwa konjektur ini salah.
contoh :
buktikan teorema ketunggalan identitas yaitu unsure identitas suatu grup adalah tunggal!
bukti :
Misalnya adalah identitas dari grup G
adalah identitas dari grup G
Ada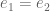
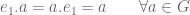
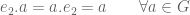
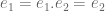
Jadi,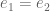
bukti :
Misalnya
Ada
Jadi,
7. Metode Pembuktian Dengan Counter Example
Untuk membuktikan suatu konjektur terkadang kita membutuhkan penjabaran yang cukup panjang dan sulit. Tapi bila kita dapat menemukan satu saja kasus yang tidak memenuhi konjektur tersebut maka pembuktian benar atau salahnya telah selesai.
Contoh
Misalkan ada konjektur berikut :”Untuk setiap n bilangan asli maka merupakan bilangan prima”
Bukti. Pernyataan ini berlaku untuk setiap bilangan asli n. Tapi bila bila ditemukan satu bilangan asli, katakan n0 dan tidak prima (komposit) maka konjektur ini tidak benar. Diperhatikan beberapa kasus berikut, untuk n = 1 diperoleh bilangan 5, n = 2 menghasilkan 17, n = 3 mengahasilkan 257 dan n = 4 menghasilkan 65537. Keempat bilangan ini prima. Coba perhatikan untuk n = 5, diperoleh = 4294967297 = (641)(6700417). Ternyata bukan prima. n = 5 merupakan contoh penyangkalan (counter example). Akhirnya disimpulkan bahwa konjektur ini salah.
8. Metode Induksi Matematika
Semua inferensi Matematika dimulai secara deduktif mengakibatkan sulitnya melakukan pembuktian secara induktsi. Untuk itu dibuatlah pendekatan langkah-langkah untuk membuktikannya. langkah dimulai dengan menerapkan n bilangan asli pertama kemedian melakukan generalisasi pada n=k dan membuktikan kebenaran n= k+1.
contoh :
langkah (a)
langkah (b)
p(n) benar untuk n = k
langkah (c)
p(n) benar untuk n = k + 1
k suku
(k + 1) suku
Cat: berdasarkan langkah (b) diperoleh
Jadi, pernyataan jumlah bilangan bulat positif dari 1 sampai n adalah n(n+1)/2 adalah terbukti benar
9. Metode Pembuktian Dua Arah
Untuk pernyataan yang berbentuk biimplikasi p<->q, pembuktian dilakukan dengan membuktikan p->q dan q->p. Pembuktian implikasi p->q dapat dilakukan dengan pembuktian no.1, 2, 3 dan lain-lain
contoh :
Buktikan, suatu bilangan habis dibagi sembilan jika hanya jika jumlah angka-angka pembangunnya habis dibagi sembilan. Bukti. Sebelum kita buktikan, dijelaskan terlebih dulu maksud dari pernyataan ini dengan contoh berikut. Ambil bilangan 135, 531, 351, 513, 315, 153, maka semuanya habis dibagi 9. Coba periksa satu per satu. Misalkan p suatu bilangan bulat, maka dapat disajikan dalam bentuk p = xnxn-1xn-2 … x2x1x0, dimana xn 0; xn-1,… x0 bilangan bulat taknegatif. Sedangkan nilai p ini dapat ditulis dalam bentuk: p = x0 + x1101 + x2102 + … + xn10n. Jumlah angka-angka pembangunnya adalah s = x0 + x1 + x2 + … + xn: Pertama dibuktikan ( ), yaitu diketahui p habis dibagi 9, dibuktikan s habis dibagi 9. Karena p habis dibagi 9 maka dapat ditulis p = 9k untuk suatu bilangan bulat k. Diperhatikan selisih p - s, p - s = x0 + x1101 + x2102 + … + xn10n - (x0 + x1 + x2 + … + xn) = (10 - 1)x1 + (102 - 1)x2 + … + (10n - 1)xn Diperhatikan bilangan pada ruas kanan selalu habis dibagi sembilan, misalnya ditulis 9m untuk suatu bilangan bulat m. Jadi diperoleh 9k - s = 9m s = 9(k - m) yaitu s habis dibagi 9. Selanjutnya dibuktikan ( ), yaitu diketahui s habis dibagi 9, dibuktikan p habis dibagi 9. Diperhatikan p = x0 + x1101 + x2102 + … + xn10n = x0 + x1(101 - 1) + x2(102 - 1) + … + xn(10n - 1) + x1 + x2 + … + xn = [x0 + x1 + x2+ … + xn] + [x1(101 - 1) + x2(102 - 1) + … + xn(10n - 1)] Karena bilangan pada kelompok pertama dan kelompok kedua habis dibagi 9 maka terbukti p habis dibagi 9
10. Metode Pembuktian Eksistensial
Ada dua tipe bukti eksitensial ini, yaitu konstruktif dan takkonstruktif. Pada metoda konstruktif, eksistensinya ditunjukkan secara eksplisit. Sedangkan pada metoda tak konstruktif, eksistensinya tidak diperlihatkan secara eksplisit.
contoh : (menyusul)






