Pembuktian Rumus Luas Jajar Genjang

Perhatikan gambar di atas.

    Gambar diatas merupakan sebuah jajar genjang dengan alas = a dan tinggi = t,,

(CARA 1) Rumus untuk mencari Luas jajar genjang = alas x tinggi = at. Untuk membuktikan rumus tersebut maka caranya adalah sebagai berikut.

     Gambar diatas adalah jajar genjang yang di bagi menjadi 3 bagian dengan masing masing bagian mempunyai luas L1, L2 dan L3. Dalam hal ini kita akan mengubah bentuk diatas dengan memindahkan bagian yang mempunyai luas L3 agar sisi miring bidang L3 berimpit dengan sisi miring bidang L1. Untuk lebih jelasnya perhatikan gambar berikut.

      Gambar diatas merupakan hasil perpindahan bidang L3 dan berbentuk persegi panjang. karena rumus untuk mencari luas persegi panjang adalah L = panjang x lebar maka rumus luas persegi panjang diatas adalah L= alas x tinggi. karena persegi panjang di atas merupakan hasil perubahan bentuk jajar genjang, maka dapat disimpulkan bahwa rumus luas jajar genjang L= alas x tinggi = at.

(CARA 2) 

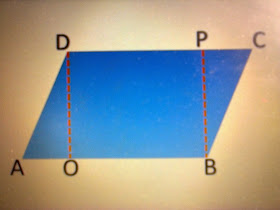
     Perhatikan gambar jajar genjang di atas. Pada gambar tersebut terdapat tiga buah bidang yaitu, BODP, AOD dan BPC.

     untuk menurunkan rumus Luas Jajagenjang adalah dengan memanfaatkan rumus luas persegi panjang dan rumus luas segitiga, yaitu :

Luas Jajagenjang = Luas persegi panjang BODP + Luas ΔAOD + Luas ΔBPC
                           = ((a-b) x t) + ½ (b x t ) + ½ (b x t )

                           = (at – bt )+ bt
                           = at – bt + bt
                           = at
Dengan, a = alas jajargenjang
              t = tinggi jajargenjang

Jadi, Rumus Luas Jajargenjang = alas x tinggi

Bagi yang ingin mendownload artikel diatas silahkan klik DISINI