beberapa waktu yang lalu saya telah memposting artikel tentang "pembuktian teorema pythagoras" yang merupakan pembuktian tertua yang berasal dari sekolah pythagoras sendiri. kali ini, saya akan kembali memberikan pembuktian teorema pythagoras namun dengan cara lainnya. cara ini dipakai oleh salah seorang astronom india yang bernama Bhaskara. Untuk lebih jelasnya bagaimana pembuktian teorema pythagoras cara Bhaskara, silahkan perhatikan uraian berikut.
Pembuktian 1
Pada
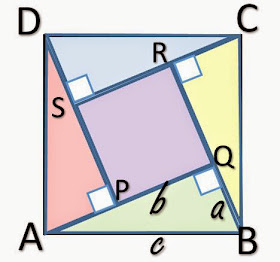
gambar di atas terdapat persegi ABCD dengan panjang sisi “c” .
kemudian di dalam persegi ABCD tersebut dibuat 4 buah segitiga siku-siku yang
sama besar dengan panjang sisi siku-siku adalah “a” dan “b”
serta panjang sisi miring adalah “c”.
Dengan memperhatikan
gambar di atas, didapatkan :
L ABCD = L PQRS + L ABQ + L BCR + L CDS + L ADP
Karena L ABQ = L BCR = L CDS = L ADP , maka :
L ABCD = L PQRS + 4 ( L ABQ)
Perhatikan
bahwa panjang sisi Persegi PQRS = ( b – a )
, berarti :
c2 = ( b – a
) 2 + 4 ( ½ ab)
c2 = ( b2
– 2ab + a2 ) + 2 ab
c2 = b2 + a2 – 2ab + 2 ab
c2 = b2 + a2 □
Pembuktian 2
Perhatikan bahwa :
∆ ABC
sebangun dengan ∆ ACD , berarti b / c = c1
/ b atau b 2 = c1
․ c . . . . . ( i )
∆ ABC
sebangun dengan ∆ BCD , berarti a / c = c2
/ a atau a 2 = c2
․ c . . . . . ( ii )
Dari ( i ) dan ( ii )
diperoleh :
a 2 + b 2 =
c2 ․ c + c1 ․ c
a 2 + b 2 =
c (c2 + c1 )
karena c2 + c1 = c , maka :
a 2 + b 2 =
c (c ) atau a 2 +
b 2 = c 2 □
Jika ingin mendownload "2 PEMBUKTIAN TEOREMA PYTHAGORAS OLEH BHASKARA (ASTRONOM INDIA) " dalam PDF , silahkan klik link di bawah ini :

No comments:
Post a Comment